Orbitas Periódicas y el Caos Hamiltoniano
Keywords:
Periodic Orbits; Hamiltonian Chaos; Non integrable systems; Symmetry Lines
Abstract
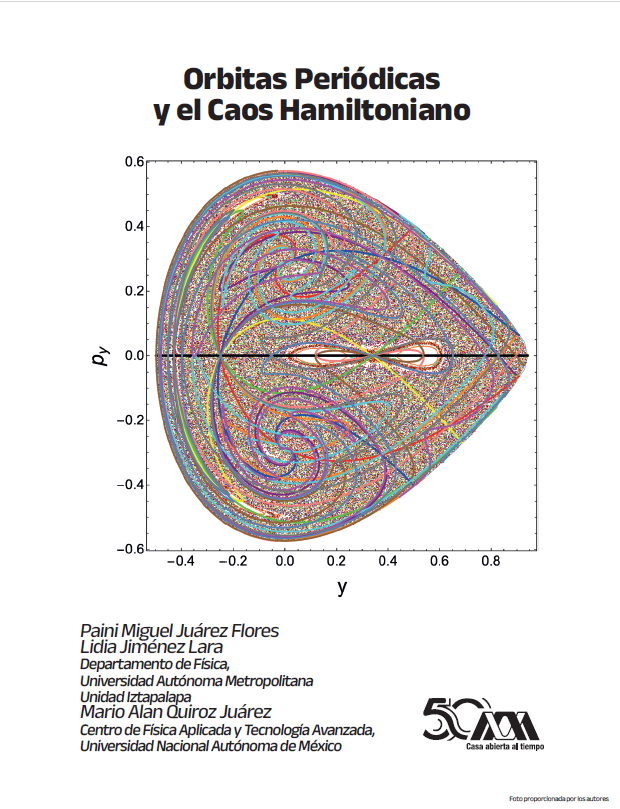
In this discussion, we explore the method of symmetry lines to identify periodic orbits in both integrable and non-integrable Hamiltonian systems. The primary focus is on non-integrable systems, which often exhibit chaotic behavior. These periodic orbits serve as reference structures around which the system’s dynamics are organized. While periodicity and chaos are usually seen as opposites, we demonstrate through examples how periodic, quasi-periodic, and chaotic orbits coexist in autonomous nonlinear Hamiltonian systems. This coexistence illustrates the complexity and richness of these systems, as well as the intricate structure of their phase space.
Downloads
Download data is not yet available.
References
Arnold, V., Kozlov, V., & Neishtadt, A., Dynamical Systems III: Mathematical Aspects of Classical and Celestial Mechanics, 3rd ed., Encyclopedia of Mathematical Science, Springer, 2006.
Contopoulos, G., Recent developments in stellar dynamics, The theory of orbits in the solar system and in stellar systems, vol. 25, pp. 3-18, 1966.
Hand, L., & Finch, J., Analytical Mechanics, Cambridge University Press, 1998.
Henon, M. y Heiles, C., The applicability of the third integral of motion: Some numerical experiments, Astron. J., pp. 69– 73, 1964.
Jiménez, L., & Escalona, B., Capítulo 7: La complejidad en los sistemas Hamiltonianos que Poincaré descubrió, Henri Poincaré y David Hilbert y los fundamentos de la física matemática moderna, UAM Iztapalapa, pp. 143-175, 2016.
Korsch, J., Jodl, H., & Hartmann, T., Chaos, Springer, 2008.
Lichtenberg, A., & Lieberman, M., Regular and Chaotic Dynamics, Applied Mathematical Sciences, 38, Springer, 1992.
Piña, E. y Jiménez-Lara, L., On the symmetry lines of the standard mapping, Physica D, 26[1], pp. 369–378, 1987.
Reichl, L., The Transition to Chaos, Springer, 1992. [10] Tabor, M., Chaos and Integrability in Nonlinear Dynamics, John Wiley & Sons, 1989.
Contopoulos, G., Recent developments in stellar dynamics, The theory of orbits in the solar system and in stellar systems, vol. 25, pp. 3-18, 1966.
Hand, L., & Finch, J., Analytical Mechanics, Cambridge University Press, 1998.
Henon, M. y Heiles, C., The applicability of the third integral of motion: Some numerical experiments, Astron. J., pp. 69– 73, 1964.
Jiménez, L., & Escalona, B., Capítulo 7: La complejidad en los sistemas Hamiltonianos que Poincaré descubrió, Henri Poincaré y David Hilbert y los fundamentos de la física matemática moderna, UAM Iztapalapa, pp. 143-175, 2016.
Korsch, J., Jodl, H., & Hartmann, T., Chaos, Springer, 2008.
Lichtenberg, A., & Lieberman, M., Regular and Chaotic Dynamics, Applied Mathematical Sciences, 38, Springer, 1992.
Piña, E. y Jiménez-Lara, L., On the symmetry lines of the standard mapping, Physica D, 26[1], pp. 369–378, 1987.
Reichl, L., The Transition to Chaos, Springer, 1992. [10] Tabor, M., Chaos and Integrability in Nonlinear Dynamics, John Wiley & Sons, 1989.
Published
2024-12-19
How to Cite
Juárez Flores, P. M., Jiménez Lara, L., & Quiroz Juárez, M. A. (2024). Orbitas Periódicas y el Caos Hamiltoniano. Contactos, Revista De Educación En Ciencias E Ingeniería, (139), 62 - 71. Retrieved from https://contactos.izt.uam.mx/index.php/contactos/article/view/469
Section
Artículos





