Orbitas Periódicas y el Caos Hamiltoniano
Palabras clave:
Órbitas Periódicas; Caos Hamiltoniano; Sistemas no integrables; Líneas de Simetría
Resumen
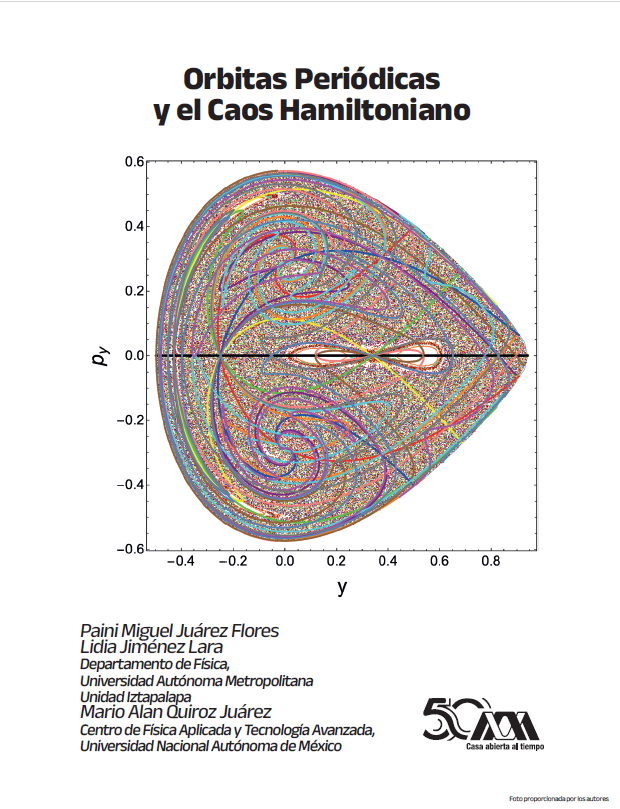
Abordamos el método de líneas de simetría que permite encontrar órbitas periódicas en sistemas Hamiltonianos tanto integrables como no integrables. Los sistemas no integrables tienen frecuentemente soluciones caóticas. Las órbitas periódicas actúan como estructuras de referencia alrededor de las cuales se organiza la dinámica del sistema. Usualmente se entienden como antónimos la periodicidad y el caos, pero aquí veremos con un ejemplo cómo coexisten las órbitas periódicas, cuasi-periódicas y caóticas en los sistemas Hamiltonianos autónomos no lineales, lo que nos permite ilustrar la complejidad y riqueza de estos sistemas y su estructura del espacio fase.
Descargas
La descarga de datos todavía no está disponible.
Citas
Arnold, V., Kozlov, V., & Neishtadt, A., Dynamical Systems III: Mathematical Aspects of Classical and Celestial Mechanics, 3rd ed., Encyclopedia of Mathematical Science, Springer, 2006.
Contopoulos, G., Recent developments in stellar dynamics, The theory of orbits in the solar system and in stellar systems, vol. 25, pp. 3-18, 1966.
Hand, L., & Finch, J., Analytical Mechanics, Cambridge University Press, 1998.
Henon, M. y Heiles, C., The applicability of the third integral of motion: Some numerical experiments, Astron. J., pp. 69– 73, 1964.
Jiménez, L., & Escalona, B., Capítulo 7: La complejidad en los sistemas Hamiltonianos que Poincaré descubrió, Henri Poincaré y David Hilbert y los fundamentos de la física matemática moderna, UAM Iztapalapa, pp. 143-175, 2016.
Korsch, J., Jodl, H., & Hartmann, T., Chaos, Springer, 2008.
Lichtenberg, A., & Lieberman, M., Regular and Chaotic Dynamics, Applied Mathematical Sciences, 38, Springer, 1992.
Piña, E. y Jiménez-Lara, L., On the symmetry lines of the standard mapping, Physica D, 26[1], pp. 369–378, 1987.
Reichl, L., The Transition to Chaos, Springer, 1992. [10] Tabor, M., Chaos and Integrability in Nonlinear Dynamics, John Wiley & Sons, 1989.
Contopoulos, G., Recent developments in stellar dynamics, The theory of orbits in the solar system and in stellar systems, vol. 25, pp. 3-18, 1966.
Hand, L., & Finch, J., Analytical Mechanics, Cambridge University Press, 1998.
Henon, M. y Heiles, C., The applicability of the third integral of motion: Some numerical experiments, Astron. J., pp. 69– 73, 1964.
Jiménez, L., & Escalona, B., Capítulo 7: La complejidad en los sistemas Hamiltonianos que Poincaré descubrió, Henri Poincaré y David Hilbert y los fundamentos de la física matemática moderna, UAM Iztapalapa, pp. 143-175, 2016.
Korsch, J., Jodl, H., & Hartmann, T., Chaos, Springer, 2008.
Lichtenberg, A., & Lieberman, M., Regular and Chaotic Dynamics, Applied Mathematical Sciences, 38, Springer, 1992.
Piña, E. y Jiménez-Lara, L., On the symmetry lines of the standard mapping, Physica D, 26[1], pp. 369–378, 1987.
Reichl, L., The Transition to Chaos, Springer, 1992. [10] Tabor, M., Chaos and Integrability in Nonlinear Dynamics, John Wiley & Sons, 1989.
Publicado
2024-12-19
Cómo citar
Juárez Flores, P. M., Jiménez Lara, L., & Quiroz Juárez, M. A. (2024). Orbitas Periódicas y el Caos Hamiltoniano. Contactos, Revista De Educación En Ciencias E Ingeniería, (139), 62 - 71. Recuperado a partir de https://contactos.izt.uam.mx/index.php/contactos/article/view/469
Sección
Artículos





